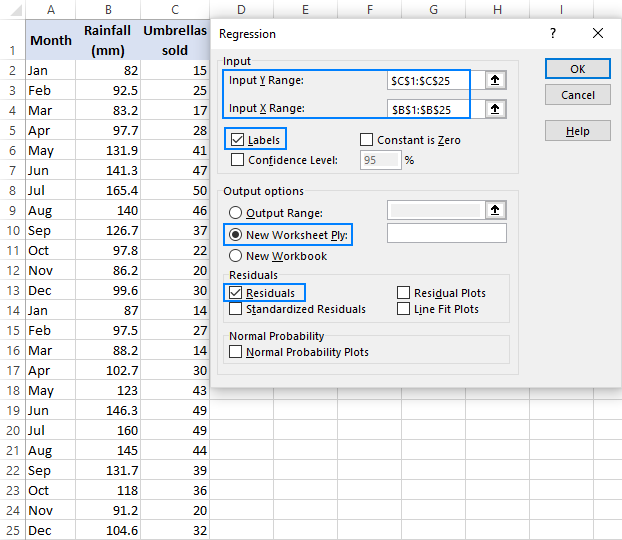
Regression analysis is generally used to see if there is a statistically significant relationship between two sets of variables. Things to Remember About Linear Regression in Excel The last method for regression is not so commonly used and requires statistical functions like slope (), intercept (), correl (), etc., to carry out regression analysis. Residuals indicate the difference between actual and predicted values. So this way, we can predict values of y for any other values of x. Now, if we wish to predict average medical expenses when age is 72: So, our regression equation would be: y= 16.891 x – 355.32. This is the same as that done by method 1 (scatter chart with a trendline). Coefficients are the most important part used to build regression equation. However, the ‘Significance F values’ indicate how reliable our results are, with a value greater than 0.05 suggesting to choose another predictor. This is generally not used for simple linear regression. Anova tells the level of variability within the regression model. Observations depict the number of model observations. Standard Error depicts the precision of regression analysis. Adjusted R Square is R Square adjusted for a number of predictors in the case of multiple linear regression. In this case, 0.57=57% of y-values are explained by the x-values. It lies between 0 and 1, with a value close to 1 indicating that the model is a good fit. R Square is the Coefficient of Determination used as an indicator of goodness of fit. It lies between -1 and 1, and its absolute value depicts the relationship strength with a large value indicating a stronger relationship, a low value indicating negative and zero value indicating no relationship. Multiple R is the correlation coefficient that measures the strength of a linear relationship between two variables. Regression Statistics tells how well the regression equation fits the data:. Now our regression analysis output will be created in a new worksheet, stating the Regression Statistics, ANOVA, residuals and coefficients. 
Select the ‘residuals’ checkbox and click ‘OK. Check the ‘Labels’ box to include headers. In the case of multiple linear regression, we can select more columns of independent variables (like if we wish to see the impact of BMI as well on medical expenses). Select the Input Y range and Input X range (medical expenses and age, respectively). Click on ‘Data Analysis’ in the ‘Data’ tab. This will add ‘Data Analysis’ tools to the ‘Data’ tab. Select ‘Excel Add-Ins’ in the ‘Manage’ box, and click on ‘Go.’. Method #2 – Analysis ToolPak Add-In MethodĪnalysis ToolPak is sometimes not enabled by default, and we need to do it manually. If the graph gets plotted in reverse order, then either switch the axes in a chart or swap the columns in the dataset. Note: In this type of regression graph, the dependent variable should always be on the y-axis and independent on the x-axis. We can improvise the chart as per our requirements, like adding axes titles, changing the scale, color and line type. Now in the ‘Format Trendline’ pane on the right, select ‘Linear Trendline’ and ‘Display Equation on Chart’. To do this, right-click on any data point and select ‘Add Trendline.’ Now a scatter plot will appear, and we would draw the regression line on this. :max_bytes(150000):strip_icc()/006-how-to-run-regression-in-excel-4690640-d95adcb0c21f414db3d162701e04575f.jpg "how to linear regression excel")
Click on ‘Insert’ and expand the dropdown for ‘Scatter Chart’ and select ‘Scatter’ thumbnail (first one). Select the two columns of the dataset (x and y), including headers. Let us first see how only age affects medical expenses. 
Now with an insight into the individuals’ characteristics like age and BMI, we wish to find how these variables affect the medical expenses, and hence use these to carry out regression and estimate/predict the average medical expenses for some specific individuals. Let us say we have a dataset of some individuals with their age, bio-mass index (BMI), and the amount spent by them on medical expenses in a month.
#How to linear regression excel download
You can download this Linear Regression Excel Template here – Linear Regression Excel Template Method #1 – Scatter Chart with a Trendline
0 kommentar(er)
